Maarten Terpstra1,2, Matteo Maspero1,2, Jan Lagendijk1, and Cornelis A.T. van den Berg1,2
1Department of Radiotherapy, University Medical Center Utrecht, Utrecht, Netherlands, 2Computational Imaging Group for MR diagnostics & therapy, University Medical Center Utrecht, Utrecht, Netherlands
1Department of Radiotherapy, University Medical Center Utrecht, Utrecht, Netherlands, 2Computational Imaging Group for MR diagnostics & therapy, University Medical Center Utrecht, Utrecht, Netherlands
The \(\ell^2\) norm is the default loss function for complex image reconstruction. In this work, we identify unexpected behavior for \(\ell^p\) loss functions, propose a new loss function, which improves deep learning complex image reconstruction performance.
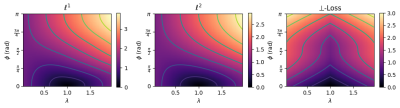
Figure 2: Simulation of loss landscapes. The loss landscapes of the \(\ell^1, \ell^2,\) and \(\perp\)-loss are shown, respectively. For every \((\phi, \lambda)\) pair, \(10^5\) random complex number pairs were generated. Contours show lines of equal loss. The figures show that \(\perp\)-loss is symmetric around \(\lambda\), whereas the \(\ell^1\) and \(\ell^2\) loss functions have a higher loss for \(\lambda > 1\).

Figure 3: Typical reconstructions. Typical magnitude reconstructions from the \(\ell^1\), \(\ell^2\) and \(\perp\)-loss networks with R=5. Top row shows magnitude target and reconstructions, with respective squared error maps below. The training with our loss function reconstructs smaller details as highlighted by the red arrows. Third row shows phase map target and reconstructions, with respective error maps below. Significant phase artifacts not present in \(\perp\)-loss are highlighted.
