1Computer Science and Artificial Intelligence Laboratory, Massachusetts Institute of Technology, Cambridge, MA, United States, 2Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA, United States, 3Centre for Medical Image Computing, University College London, London, United Kingdom, 4A. A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital, Charlestown, MA, United States, 5Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 6Institute for Medical Engineering and Science, Massachusetts Institute of Technology, Cambridge, MA, United States

Figure 4. Top: Example reconstructions with motion induced at 3% of scanning lines. The Interleaved and Alternating architectures more accurately eliminate the 'shadow' of the moved brain and the induced ringing and blurring compared to the single-space networks.
Bottom: Comparison of all four network architectures on test samples with motion at varying fractions of lines. For nearly every example, the joint architectures (Interleaved and Alternating) outperform the single-space baselines.
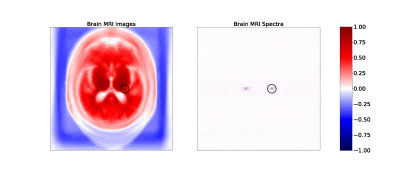
Figure 1. Maps of correlation coefficients between a single pixel (circled) and all other pixels in image (left) and frequency (right) space representations of the brain MRI dataset (click to view an animation of correlation patterns at several pixels). Both maps show strong local correlations useful for inferring missing or corrupted data. Frequency space correlations also display conjugate symmetry characteristic of Fourier transforms of real images.
