Simon Weinmüller1, Hoai Nam Dang1, Alexander Loktyushin2,3, Felix Glang2, Arnd Doerfler1, Andreas Maier4, Bernhard Schölkopf3, Klaus Scheffler2,5, and Moritz Zaiss1,2
1Neuroradiology, University Clinic Erlangen, Friedrich-Alexander Universität Erlangen-Nürnberg (FAU), Erlangen, Germany, 2Max-Planck Institute for Biological Cybernetics, Magnetic Resonance Center, Tübingen, Germany, 3Max-Planck Institute for Intelligent Systems, Empirical Inference, Tübingen, Germany, 4Pattern Recognition Lab Friedrich-Alexander-University Erlangen-Nürnberg, Erlangen, Germany, 5Department of Biomedical Magnetic Resonance, Eberhard Karls University Tübingen, Tübingen, Germany
1Neuroradiology, University Clinic Erlangen, Friedrich-Alexander Universität Erlangen-Nürnberg (FAU), Erlangen, Germany, 2Max-Planck Institute for Biological Cybernetics, Magnetic Resonance Center, Tübingen, Germany, 3Max-Planck Institute for Intelligent Systems, Empirical Inference, Tübingen, Germany, 4Pattern Recognition Lab Friedrich-Alexander-University Erlangen-Nürnberg, Erlangen, Germany, 5Department of Biomedical Magnetic Resonance, Eberhard Karls University Tübingen, Tübingen, Germany
Using analytic
signal equations combined with neural network reconstruction allows fast, fully
differentiable supervised learning of MRI sequences. This forms a fast
alternative to the full Bloch-equation-based MRzero framework in certain cases.
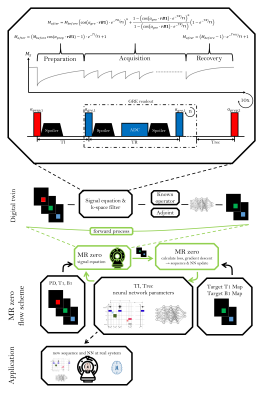
Figure 1: Schematic
of the MRzero framework. Topmost part: An MR image is simulated for given
sequence parameters and Bloch parameters (PD, B1 and T1) with an analytic signal equation. The evolution of the signals
are mapped pixelwise to B1 and T1 values with a NN. The output is compared to
the target (B1 and T1 value) and gradient descent optimization is performed to update sequence
parameters TI, Trec, TR, $$$\alpha_{gre}$$$, $$$\alpha_{prep}$$$ and NN parameters.
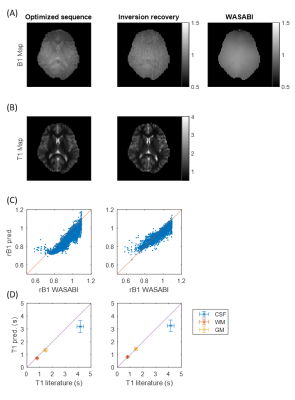
Figure 4: Pixelwise evaluation
of the NN-predicted B1 (A) and T1 (B) maps for the optimized sequence (first column)
and the inversion recovery (second column). B1 map from the WASABI measurement
as reference (third column). Correlation between
WASABI and optimized sequence with correlation coefficient R=0.88 and
correlation between WASABI and inversion recovery with correlation coefficient
R=0.90 (C). Comparison of obtained T1 values for different tissue ROIs with
literature values (D).