Figure 2: Results of the MRE acquisition depicting the z-component of the curl of the displacement vector in the pure ultrasound gel and in the ultrasound gel with the embedded scattering structure.

Figure 5: Dispersion curves (with a power law fittings) and the corresponding frequency evolution of the phase angle for the pure ultrasound gel, ultrasound gel with embedded fractal structure, and a bovine tissue specimen. Magnitude coronal sections of the three specimens are shown on the first column.

Figure 2. The reconstruction procedure of the proposed method. In the first step, the acquired spokes are rearranged to 8 k-spaces belonging to different phase images. The k-data encoded by negative MEGs are then resorted and concatenated to the data with positive MEGs encoding to form a pseudo continuous wave. In the second step, the rearranged k-data are reconstructed simultaneously. The modified TV transform and temporal FFT are the sparsifying transforms.

Figure 1. Sequence diagram of the MRD-MRE. The motion encoding gradient (MEG) G_e is applied under a static state and decoded by all the following motion decoding gradients (MDG) G_dn. With a golden angle radial sampling pattern, the spokes belonging to different phase offset are acquired continuously and rearranged after the scan for reconstruction of different phase images. The time interval Δt between the trigger time and MDG determines the phase offset of each spokes.

Figure 3: Results of free-breathing TURBINE-MRE from a healthy volunteer. The animation shows the magnitude, x-, y-, z- components of curl wave information, and stiffness maps at 5 respiratory states. The contours on the wave images and stiffness map delineate the boundaries of the liver and other organs. (High definition movie can be found at https://youtu.be/yw9yOhGvAi8 )

Figure 2: Respiratory motion estimation from k-space data. (a) Flow chart for respiratory motion estimation. (b) TURBINE k-space trajectory. The center Kz lines (dashed line) from all EPI blades were taken out for motion estimation. (c) Mzt: 1D z-projection of whole imaging volume along time. PC: The largest principal component of Mzt. PCbc block-wise baseline-corrected PC. Each colored ribbon marks a MRE direction as a block. The respiratory motion (blue) was estimated from all channels using a coil clustering method and was consistent with the respiratory bellows signal (orange).

Figure 2: Representation of one segment of the UTE-based MSPrep-MRE pulse sequence and delimitation of its three main parts: the motion preparation and residual magnetization spoiling, the train of MRI repetitions and the stand-by time (200 ms and 150 ms for HoP and HeP acquisitions respectively).

Figure 4: MR magnitude images, wave maps directionally filtered along the up-to-down direction and Young’s modulus maps obtained for the heterogeneous phantom (HeP) at 150 and 180 Hz. Two sagittal planes with three and two inclusions are presented. A Maximum Intensity Projection (MIP) in the coronal view clearly depicts the five inclusions.

Bar chart displays group viscoelastic shear stiffness values in three groups for the whole brain, the cerebral white matter and the cerebral cortex, with significance difference between groups indicated with * (p < 0.05). Stiffness maps were registered to the MNI standard space template and averaged across subjects of same age group.

Bar chart displays group viscoelastic shear stiffness values in three groups for the subcortical grey matter structures including the amygdala, hippocampus, caudate, putamen, pallidum and thalamus, with significance difference between groups indicated with * (p < 0.05). Stiffness maps were registered to the MNI standard space template and averaged across subjects of same age group.

Figure 4: Magnitude images with a resolution of 1x1mm and the waterfall diagram along the indicated path (pink) (A) The location of the transducer underneath the torso is indicated by the block and the direction of vibration by the arrow in the magnitude image.(B) Magnitude image at the start of diastole with the wave plane through slices (pink cross) and the path for the waterfall-diagram (C) Magnitude image of the rats’ shape of the heart at end diastole, showing the left and right ventricle. (D) Waterfall-diagram, showing the travelled distance over time along the path indicated in B.

Figure 1: TTL: Transistor-transistor logic trigger; A) ECG+respiratory gated acquisition. Delaying 100 ms each mechanical push (200 Hz) trigger with respect to R spike (TTL) ensures consistent diastolic acquisition. 10 acquisition repetitions with an increment of 0.7 ms delays among them artificially lower temporal resolution to 0.7 ms. B) Diagram of the anesthetized rat and how thoracic excitation is executed for generation of internal shear waves that travel towards and through the heart.

Figure 1. Representative cases. Fibrosis stage F0: 51-year-old female healthy volunteer. F2: 31-year-old female patient with autoimmune hepatitis. F3: 53-year-old female patient with toxic liver disease. F4: 73-year-old female patient with diffuse liver metastases. For presented cases with F0/F2/F3/F4, fluidity (φ) was 0.60, 0.62, 0.63, 1.01 rad, and shear-wave speed (SWS) was 1.46, 1.64, 1.91, 3.22 m/s, respectively.

Figure 2. SWS Dispersion. Dispersion of stiffness (SWS) for F0, F1-3, and F4 is displayed over single frequencies from 35 to 60 Hz.

Figure 4. The Locally Weighted Scatterplot smoothing of liver stiffness measurement (LSM) versus proton density fat fraction (PDFF) in all cases (a), and within each fibrosis stage (b). In the gray area where PDFF is less than 5% (mostly S0 cases), there are many F3 and F4 patients, and the slight decrease in LSM in patients with cirrhosis is due to the biased distribution of high LSM and low PDFF, also known as the “burned-out” NASH.

Table 1. Results of linear regressions with liver stiffness measurement as the dependent variable in patients with diagnosed steatosis (PDFF≥5%), and in different subgroups.

Figure 1: Example pre- and post-immunotherapy images from an 83 yr old female with hepatitis B. A 7cm hepatocellular carcinoma is seen in the right lobe (white outline). A moderate decrease in tumor stiffness (TS) is noted post immunotherapy however liver stiffness (LS) remains unchanged. At resection the tumor was 100% necrotic.

Figure 2: Boxplot showing elevated baseline stiffness in tumors with high density of tumor infiltrating lymphocytes at resection.

.

.

A Representative c-map showing the DG mask and its diminution in a pixel-wise manner. B there is significant decrease in stiffness (c in m/s) when down-sizing the mask. C Representative ϕ-map showing the erosion of the DG mask in a pixel-wise manner. D There is significant decrease in the loss angle, when the mask is eroded. **** ≦ 0.0001, *** ≦ 0.001, ** ≤ 0.01, ≤ 0.05*

A AFM set-up on the left, on the right a sketch, the brain slice is placed in a petri dish on the sample scanner stage of the AFM. The AFM-cantilever is probing the brain slice from above. An upright fluorescent microscope allows imaging the GFP-signal, optical and AFM-Image are registered with pixel-precision. B Exemplary fluorescent image of a brain slice overlaid with the local Young‘s Modulus. C The SGZ (high fluorescence signal) is softer compared to neighboring regions(low fluorescence signal) in the dentate gyrus, paired Wilcoxon-test was performed. *** ≦ 0.001

Mean MRE magnitude, maps of |G*| and φ and the registered mean diffusivity (MD) in two selected slices for one patient from each subgroup. Top rows group 1 (2x2x2 mm³ voxel size). Bottom rows group 2 (1.5x1.5x2 mm³ voxel size). Lesion masks are demarcated in red and the masks for the surrounding tissue is demarcated in green. Grayscale colorbar (black to white) is as follows: |G*| in Pa: 0 – 2000, φ in rad: 0.16 – 1.6, MD in 10^-3*mm*s^-1: 0.2 – 1.4.

Relative intensity difference (rID) of lesions compared to surrounding tissue for group 1 (2x2x2 mm³ voxel size) shown as histogram (top) and bar-chart (bottom) for |G*|, φ, T2w intensity from mean MRE magnitude image and mean diffusivity (MD). Mean ± SD of rID are given in the figure. rID thresholds for bar-charts are 5%.

Figure 1: Axial maps at slices 12, 25, 28 and 40 of the absolute variation of the MR signal lifetime, ΔT₂, between 0° and 17° positions (top row). ΔT₂ is essentially zero everywhere but in the CSF and orbital compartments where it exhibits a clear T₂ decrease in HDT position. Shear velocity, V_s, and viscoelastic moduli, G’ and G”, maps reveal a global mechanical increase between 0° supine and 17° HDT in the cerebral tissues (bottom rows).

Figure 2: Relative variation of the median MR transverse relaxivity (R₂ = 1/T₂) (black), of the mean shear velocity ‹V_s› (green), the mean shear elasticity ‹G’› (dark orange) and shear viscosity ‹G”› (light orange) across the inferior-superior axial slices. While T₂ positively varies only locally in the CSF and orbital compartments, ‹V_s›, ‹G’› and ‹G”› increase everywhere in the cerebral tissues, remain rather constant in cerebellum and decrease around the tentorium.

Figure 3: Shear wave speed maps of the zebrafish brain and skeletal muscle, with slice a) being most caudal and slice d) most cranial. The optic tectum is marked in green, the telencephalon in blue and a representative slice through the muscle in red.

Figure 4: Mean SWS of different brain regions and back muscle of sampled zebrafish. Muscle tissue could not be measured in all fish due to placement in the glass tube. While we found no statistical difference between identified brain regions, a clear difference between the full brain and skeletal muscle tissue was found using the Wilcoxon rank sum test. *indicates p<0.05.

Figure 1. Coefficient of variation (CV) vs. magnitude of the complex shear modulus (|G*|) for healthy (blue circles) and cancerous segments (red crosses). The line shows linear correlation with r = -0.48 and p < 0.001.

(a) Group values of SWS of aortic wall of controls and AAA. (b) Regional analysis based on Elastica-van-Gieson stainings of three AAAs for regions with high (red ROIs) and low content (blue ROIs) of extracellular matrix (ECM) components.

Experimental setup. (a) Abdominal aorta samples of control mice and mice with AAA were transferred in glass tubes with an inner diameter of 3.2 mm and embedded in ultrasound gel (details see text). (b) Upper row: transducer system for vibration generation with inserted sample tube. Main components of the transducer system include a piezo actuator which is connected by a transducer rod to a movable sample holder. Lower row: position of the transducer system in the quadrature volume coil with inner diameter of 20 mm.

Figure 1: Estimated wavelength ($$$\lambda$$$) overlaid on high-resolution T1 MPRAGE for MRE sequences obtained at 2.5 mm (left), 2.0 mm (middle), and 1.5 mm (right) isotropic resolutions on two healthy adult subjects.

Figure 3: Mean and standard deviation of the estimated wavelength (mm) in each of the left and right hemisphere lateral occipital cortex ROIs and adjacent white matter, depicted in Figure 2, from MRE scans done at 2.5, 2.0, and 1.5 mm resolutions, respectively, for each of the two subjects.

Figure 3. Receiver Operating Characteristic (ROC) of NASH prediction models and effect test for various models. ROC analyses for the diagnosis of NASH based on the nominal logistic fit models. PDFF_liver, fat fraction of liver; SS_liver, liver stiffness; SS_fat, subcutaneous fat stiffness. *, p < 0.05.

Figure 1. Examples of ROI placement to measure liver and fat shear stiffness and fat fraction. The white area (A) and pink area (B) represent the ROIs used to report the shear stiffness and fat fraction, respectively, for subcutaneous adipose tissue. The yellow areas (A and B) represent the ROIs for the liver.

Figure 1: Transversely isotropic (top row) and isotropic (bottom row) NLI-MRE reconstructions from a healthy volunteer. DTI fiber orientations are indicated by black lines. The results show the storage modulus ($$$\mu_R$$$) and loss modulus ($$$\mu_I$$$) distributions for the two reconstructions, as well as the distribution of the OSS-SNR. (Note that the color scales differ between isotropic and anisotropic reconstruction images.)

Figure 2: Transversely isotropic (top row) and isotropic (bottom row) NLI-MRE reconstructions from a repeat imaging exam of the same healthy volunteer shown in Figure 1. DTI fiber orientations are indicated by black lines. The results show the storage modulus ($$$\mu_R$$$) and loss modulus ($$$\mu_I$$$) distributions for the two reconstructions, as well as the distribution of the OSS-SNR. (Note that the color scales differ between isotropic and anisotropic reconstruction images.)

Figure 2. (Left to right) Anatomical T2w water image, MRE magnitude image, MRE phase difference image, strain images and N-strain map.

Figure 4 N-strain maps and the N-strain values vs. volunteer’s age.

Figure 2: Correlation curves of Gd and Ishak fibrosis score vs DPVP, with the relative linear fit, the R-squared value and the respective Spearman's coefficient of rank correlation (rho).

Figure 1: Anatomy, y-component of the curl of the displacement vector, shear stiffness and viscosity, for two selected patients with low (Pat A) and high DPVP (Pat B) (Pat A: DPVP 3mmHg and fibrosis score 1, Pat B: DPVP 28 mmHg and fibrosis score 6).

Figure 1. Flow Diagram of the Proposed Aortic MRE Inversion Strategy.

Figure 4. Aortic Stiffness in Healthy Subjects and in AAA Patients. MRE wave images were overlaid on the anatomical image for each subject. Higher stiffness was observed in senior healthy subject (a vs. b). For patients, vascular surgeons were blind to AAA stiffness measurements. EVAR repairs were recommended to the patients based on AAA diameters and growth rate. In patients with small or stable AAAs (c, d and f), AAA stiffness was considerably higher than that in patient who has a rapidly growing AAA (e). All stiffness estimation were performed using the proposed inversion technique.

Figure 1: Representative stiffness |G*| maps (both coronal and axial views) from a healthy control (A, B) and HIV+ subject (C, D) with respective probability histograms (E) overlayed on respective T1w images. Intensity scales are also shown. HC: healthy control; HIV+: HIV-infected individual.

Figure 4: Significant |G*|, and f_ISO changes in GM and WM ROIs: The group comparison for significant regions of (A) WM, (B) Subcortical GM and (C) Cortical GM are shown. Significant regions for A, B and C are overlayed with respective legends in (D) on standard space with Coronal, Sagittal and Axial view. Relevant parameters are |G*|, $$$\phi$$$ and f_ISO, only significant changes are shown.

Simulated data with noise. Top) Left: Correlation with no filter. Middle: Correlation with LPS filter. Right: Correlation with neural net denoising. Bottom) from left to right: Original displacements, no filter, LPS filter, neural net denoising.

Sagittal view of calculated x component of the curl from in vivo data. Left: No Filter. Middle: LPS filter. Right: Neural net denoised.

Figure 2: Shear modulus and viscosity maps for the cylinder model when no noise is added. (a) The true maps, (b) the reconstruction results of the conventional method, and (c) the reconstruction results of the proposed method. The table at the bottom shows the normalized L2 errors associated with each method.

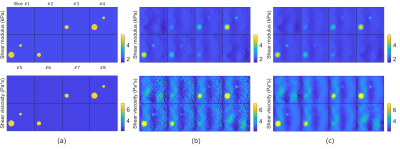
Figure 4: Shear modulus and viscosity maps for the sphere model when 1% Gaussian noise is added. Each figure shows results for all eight slices. (a) The true maps, (b) the reconstruction results of the proposed method with no regularization and (c) the reconstruction results of the proposed method with TV regularization.

Figure 1. Representative wave motion, damping ratio, and shear stiffness maps from each of the four phantoms with varying LPAA concentration from 0% to 6%.

Figure 3. Loss modulus frequency dependence. The four LPAA/PAA phantoms exhibit increasing loss moduli with increasing frequency from 600 to 900 Hz, indicative of viscoelastic behavior.

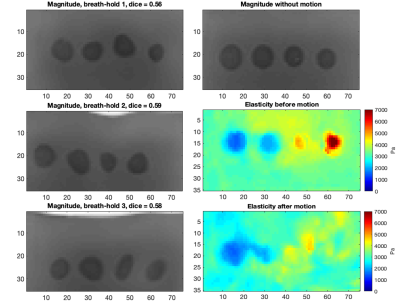
Figure 5: Magnitude images for one extreme case for each breath-hold at the highest simulated motion level and the original magnitude image for reference. The average Dice score over the breath-holds was 0.58. The elasticity maps before and after motion are also shown.

Figure 4: Violin plots comparing elasticity for all cases within each region to the ground truth (GT) for increasing motion. The average Dice overlaps between regions before and after motion are shown in blue. A table of the bulk motion and deformation applied for each motion level is also shown.

Comparison of the proposed phantom with in vivo literature data and conventional phantoms by means of shear wave speed (SWS) and penetration rate (PR). The CIRS phantom showed no measurable shear wave damping (due to an inverse relation between damping and PR, this corresponds to an infinity PR). Therefore, the PR for CIRS phantom was not shown.

Setup and post processing for USE and clinical MRE. A vibration plate was inserted in the phantom to create plane shear waves. Shear wave fields for all vibration frequencies are acquired within the $$$x-z$$$-plane. After frequency selection by Fourier transformation a profile was drawn parallel to the wave propagation (shown wave fields based on MRE). Viscoelastic properties (shear wave speed, penetration rate) are obtained by fitting profile data (circles) with a damped complex shear wave (solid lines).

Figure 2. Water images, fat fraction maps, wave images and elastograms in four subjects.

Figure 3. Fat fraction maps of lower-extremity with actuator turned off and on in four subjects.

Fusion images of stiffness map and T2-weighted images of the liver in 11 years old boy who had nonalcoholic steatohepatitis. His fat signal percentage in the liver MRI was 51%, which was above the normal limit of 6%. (a-d) Images from 20% driver power amplitudes showed mean liver stiffness of 1.9 kPa in the area of 122.5 cm². (e-h) Images from 56% driver power amplitudes showed mean liver stiffness value of 2.3 kPa in the area of 74.5 cm²

Fusion images of stiffness map and T2-weighted images of the liver in 11 years old girl who had the Kasai operation from biliary atresia. (a-d) Images from 20% driver power amplitudes showed mean liver stiffness of 5.0 kPa in the area of 63.9 cm². (e-h) Images from 56% driver power amplitudes showed mean liver stiffness value of 4.7 kPa in the area of 23.6 cm²

SWS maps for OMME (MEGs=4,8,16,32mT/m) and Laplace and Flynn unwrapping (MEG=32mT/m) at different slices. The anatomical reference from MRE magnitude is included (region of interest demarcated in red for noise estimation). Red arrows indicate where OMME shows greater contrast in the SWS map. A) Volunteer 1 for vibration frequency 25Hz at two different slices. Grayscale ranges from 0.3-1.8m/s. B) Volunteer 2 for vibration frequency 30Hz at two different slices. Grayscale ranges from 0.2-2.2 m/s.

Multiple motion encoding reconstruction in the phantom for two MEGs 8 and 16 mT/m and three MEGs 8, 16 and 32 mT/m in comparison to phase contrast images. Color scale is set in the interval 80% of the dynamic range of the MEG=8 image. Large positive values are colored in yellow and negative values in blue, while green being zero. The bottom left image shows the T2 weighted MRE magnitude as geometric reference.

Figure 5: Simulated data with added noise (a) Elastograms (with smoothing) for added noise with MM-SNR level= 5, 10, 20, 30, 40 and 50 (chosen to approximately match the acquired data); (b) mean |G*|^SM over left and right kidney volumes versus MM-SNR, for 60 Hz, and compared to ground truth value (dashed line); (c) similar to (b) but for 90 Hz. (Eroded masks are applied for display and for mean values.)

Figure 4: Simulated MRE elastograms (generated by direct inversion on the simulated displacements) with no added noise for varying voxel dimensions, with mean ± standard deviation |G*| over kidney volume, without smoothing and with smoothing of the displacements with a 3D box filter, and % difference of mean with ground truth. Eroded masks are applied for display and mean value calculations, to remove edge values which are affected by errors at the simulated kidney boundaries.

Figure 4. a) Example T2 weighted image with the SWS map on the pancreas (top left) b) and SWS map (bottom left) in one volunteer. c) The average SWS per scan-protocol. The SWS is higher for 50Hz as expected compared to scans using 40Hz.

Figure 1. a) Example shear wave amplitude map. The line-profile is given in black. b) The average amplitude measured in the pancreas head plotted for each volunteer for each scan. c) The shear wave amplitude was measured and a line-profile was made from the liver to the pancreatic head. The blue line indicates the line-profile for a protocol with a frequency of 40Hz and the red line is for a frequency of 50Hz.

Figure 1. (a) A 3D rendering of the electromagnetic actuator for brain MRE in working position. The vibration plates wrap around the human head inside a head coil. (b) A volunteer wearing the actuator before moving into the MR bore for MRE. The vibration plates are fixed on the head with soft bandages. The part of the actuator that extrudes out of the head coil is 7.5 cm in height, leaving enough space for positioning.

Figure 5. The first line and the second line are the typical MRE results from the phantom and a volunteer, respectively. Column 1 is the magnitude image. Column 2-4 are the real part of the first harmonic component of the displacement field in x, y, and z direction, respectively. Column 5 is the LFE inversion results after smoothing. The locations of these three agar inclusions are indicated by white circles.

Results from MDEV (|G*|) and 2D and 3D k-MDEV (SWS) inversion in different slices (1.5-Tesla). Magnitude images are shown on the left side together with segmented regions for white matter (red) and gray matter (yellow). The last row shows results for the measurement at 3.0-Tesla with 1.6x1.6x2mm³ voxel size. Increased resolution allows to easily identify anatomical regions in deep gray matter characterized by stiff properties such as the putamen and caudate nucleus (indicated by arrows).

2D and 3D k-MDEV. The phase of the MRE data is smoothed (Butterworth lowpass, threshold 250 m^-1, order 3) and the harmonic wave field is extracted using the Fourier transform. For 3D, inter-phase discontinuities (IPD) and slice offsets [13] are removed as shown in the sagittal view. A bandpass filter (Butterworth, lower threshold 15 m^-1, upper threshold 200 m^-1, order 3) suppresses compression waves and the remaining shear wave field is directionally filtered in 8 (2D) or 20 (3D, right, dodecahedron) directions. SWS is reconstructed from the phase gradient in 2D and 3D.

Figure 2: (left) Example of 4-channel input image; (right) Corresponding 2-channel output predicted by the U-net; (center) U-net architecture – blue boxes represent feature maps with the number of channels denoted on top of the box. The arrows represent operations as described by the legend.

Figure 3: (top) Comparing manual mask with deep learning method mask: agreement (green) and overshoot (blue) and undershoot (red) of the deep learning method. Elastograms of the manual mask (middle) and deep learning mask (bottom). Both the manual and the deep learning mask have similar elastograms.

The piecewise smooth inversion produces the best contrast to noise ratio (CNR) for inclusions in the brain simulating phantom. The piecewise smooth inversion produces the best CNR in 4 of the 6 inclusions and is a close second in a fifth. The only inclusion where the piecewise smooth inversion did not perform well was difficult for all inversions, as no inversion produced a CNR better than 1.

Different inversion material property assumptions produce no difference in repeatability. While stiffness maps in an individual case are appreciably different (bottom row), there is no significant difference in coefficient of variation (CV) between the inversions in any of the 35 gray matter regions of interest. The box plot (line=median, box edges = 25th/75th percentiles, whiskers=extremes, +=outlier) shows the mean of the mean CVs in the 35 regions for the four inversions in 10 subjects.

Representative brain images obtained by MRE and IR-MRE in the same volunteer. The magnitude signals in IR-MRE show solid tissue without freely moving water, leading to significantly improved depiction of fluid-solid boundaries in SWS maps (arrows). Note that sulci and ventricles are narrower in IR-MRE than MRE due to suppressed phase discontinuities, similar to the phantom experiments shown in Figure 3.

Group values of parameters quantified in this study. *** p < 0.001.

Figure 2: (A) AP and LR excitation wave characteristics for (matching slice, repetition): motion fields, wave propagation/polarization directions, isotropic inversion shear stiffness. (B) 3D vectors display average directions of wave propagation and polarization in the CST vs. fiber orientation (DTI). Light and dark arrows represent repetitions and averaged across all repetitions, respectively. We observe similar wave propagation directions between AP and LR excitations. Wave polarization directions are visibly differentiable and distinct from propagation.

Figure 1: Schematic of the custom actuator design orientations (A, B, C) and a picture of the set-up inside the 20 channel head coil (D). The design allows the actuator to rest against the side of the subject’s head and is adjustable for different head sizes; it can be configured before the subject is laying in the coil which reduces set-up time and variability.

Elastograms with overlying confidence maps obtained with 2D GRE (A), 2D EPI (B), and 3D EPI (C) MR elastography techniques in a 70-year-old male patient with non-alcoholic fatty liver disease. The liver parenchyma available for LSM measurement was significantly larger with 3D MRE.

Bland-Altman plots showing magnitude of variation of LSMs between 3D EPI and 2D GRE (A), and between 3D EPI and 2D EPI (B). Arbitrary lines for 0.5 kPa and 1 kPa difference in LSMs are drawn.

Figure 2. A) Phase image of the composite excitation (rad). B) Then separed in phase images (rad) of every frequency component extracted after temporal fourier transform: top, 400 Hz; bottom, 600Hz. C) G' elastograms (kPa) reconstructed for each frequency component.

Figure 1. Experimental setup: the shear wave propagates in the phantom along the x-axis. The shear wave-dephasing angle is defined as θⁱ=2πxⁱ/λ with xⁱ representing a specific position.

Figure 3. (a) The experimental and fitted ramp and relaxation curves from indentation tests. (b) Wave propagation images of MRE from 6 different actuation frequencies.

Figure 4. Comparisons of the shear moduli of the gel phantom based on indentation and MRE measurements.

Fig.2: Comparison of reconstructed wavelength maps (λ in mm) of a healthy volunteer acquired at three different spatial resolutions: (a) 2.5 mm isotropic; (b) 2 mm isotropic; and (c) 1.5 mm isotropic voxels. Axial T1 image of 0.5 mm in-plane resolution of the matching slice is shown in (d). Median and standard deviation of valid brain region voxels in the slice are shown on top right corner.

Fig.1: Schematic of fMRE data acquisition with interleaved stimulus paradigms, i.e., PAR1 & PAR2, each containing 9 slices and 8 wave phases. A trigger signal is sent out at the beginning of each block shown to synchronize the k-space acquisition with mechanical vibrations for both paradigms with the loop hierarchy. This block is repeated for each k-space line acquisition and MEG-encoding direction. For fMRE scans with functional activation, a stimulus will be switched ON and OFF in sync with PAR1 and PAR2 sequence timing. In this study, no stimulus is used for either PAR1 or PAR2.

Figure 3: Representative slice for each subject investigated showing each of the three anisotropic material parameters: μ, φ, and ζ.

Figure 4: Representation of the three anisotropic material parameters (μ, φ, ζ) in WM tracts: corpus callosum (CC), corona radiata (CR), and superior longitudinal fasciculus (SLF).