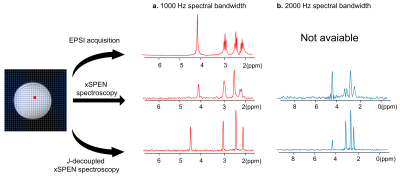
-
ORYX-MRSI: A data analysis software for multi-slice 1H-MRSI
Sevim Cengiz1, Muhammed Yildirim1, Abdullah Bas1, and Esin Ozturk-Isik1
1Biomedical Engineering Institution, Bogazici University, Istanbul, Turkey
Oryx-MRSI is a fully automated software for a comprehensive analysis of multi-slice proton magnetic resonance spectroscopic imaging (1H-MRSI) data.

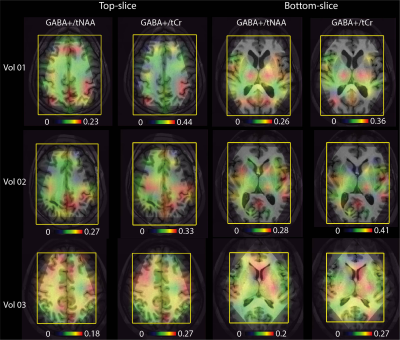
fCSF corrected NAA concentration map and its overlay onto reference T2w MRI (figure 5a) and ROI analysis of an example dataset on 400 brain parcellations defined on 17 rs-fMRI networks (figure 5b).

Segmentation module shows fCSF, fWM and fGM maps for a selected metabolite (NAA+NAAG) at different slices.
-
ProFit-v3: accuracy and precision evaluation of a new spectral fitting software
Tamas Borbath1,2, Saipavitra Murali-Manohar1,2, Johanna Dorst1,3, Andrew Martin Wright1,3, and Anke Henning1,4
1High-field Magnetic Resonance, Max Planck Institute for biological Cybernetics, Tübingen, Germany, 2Faculty of Science, University of Tübingen, Tübingen, Germany, 3IMPRS for Cognitive & Systems Neuroscience, Tübingen, Germany, 4Advanced Imaging Research Center, UT Southwestern Medical Center, Dallas, TX, United States
The newly developed ProFit-v3
fitting algorithm, including an adaptive baseline stiffness control and a new
cost function, was evaluated for accuracy and precision using both simulated
and in vivo spectra. Fitted metabolite concentration results were also compared
against LCModel.

Fig. 2: Fit results for the baseline
simulations are shown. The blue line shows the
input spectrum; the black line the input baseline. Fitted baselines (dashed
lines) and resulting residuals (continuous lines) are shown in red for LCModel
and purple for ProFit-v3. Offsets used for plotting are indicated on the right
of each subplot. Inlays show the mAIC
curves for the ProFit-v3 fitting. These spectra show
a simulated zero baseline, an in-phase (φ0 = 0°) and an out
of phase (φ0 = 90°) lipid peak at 1.3 ppm, but also an extracted
baseline from a previous LCModel fit of an in vivo spectrum.
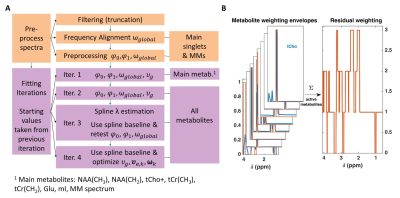
Fig. 1 A:
The ProFit-v3 algorithm is depicted with the successive optimization steps:
first preprocessing steps affect the spectrum to be fit while the fitting
iterations optimize the linear combination of the basis sets. In later
iterations, more metabolites are added, and additional metabolite specific local
degrees of freedom are allowed while keeping the previously optimized global
parameters. B: Metabolite weighting
envelopes are displayed in red. Summing the weights of active metabolites for
the fit iteration gives the weights of the spectral residual RX shown on the right.
-
Reproducibility and Coverage of Human Whole-brain 1H FID MRSI at 9.4 T after Processing Pipeline Optimization
Theresia Ziegs1,2, Andrew Martin Wright1,2, and Anke Henning1,3
1MRZ, MPI for Biological Cybernetics, Tuebingen, Germany, 2IMPRS for Cognitive and Systems Neuroscience, Tuebingen, Germany, 3Advanced Imaging Research Center, University of Texas Southwestern Medical Center, Dallas, TX, United States
Fully sampled 1H FID MRSI data were acquired at
9.4 T. An optimized processing pipeline lead to high quality concentration maps for tCr, tCho, NAA, Glu,
and mI reflecting the expected concentration difference in gray and white
matter for the major part of the brain.

Figure 4: 3D concentration maps for tCho/tCr,
Glu/tCr, NAA/tCr, mI/tCr in arbitrary units showing the brain coverage achieved
in this study with the optimized set-up using L2-regularization and including a
simulated macromolecular baseline in the LCModel fit. The metabolite maps are
underlayed with the anatomical images.

Figure 5: Mean number of voxels fitted
with CRLB < 100 % for each slice for NAA and Glu for one measurement of all
volunteers. The test-retest figure in b) shows the mean concentration for each
slice. Data is shown for all five volunteers and five different metabolites
(Cho = red dots, NAA = black dots, tCr = green dots, Glu = purple dots, mI =
blue dots). The black line is the curve fitted to the data with y = 0.96x +
0.03 and r2 = 0.94; the gray dotted line is the identity line with y = x. In c)
the absolute difference of the dots in the test-retest figure to the ideal case
of y = x is shown for five metabolites.
-
Reproducibility of High-Resolution 1H-MRSI at 7T Using SPICE
Pallab K Bhattacharyya1, Rong Guo2, Yudu Li2, Yibo Zhao2, Zhi-Pei Liang2, and Mark J Lowe1
1Cleveland Clinic Foundation, CLEVELAND, OH, United States, 2University of Illinois, Urbana, IL, United States
1H SPICE was implemented at 7T and reproducibility of the technique was demonstrated at 3×3×3 mm3 spatial resolution.

Fig. 3. In
vivo scan-rescan spectra from 4 voxels within the red box.

Fig. 5. In vivo scan-rescan reproducibility:
scan-rescan voxel-wise concentration correlation plots ((a), (b) and (c)),
Bland Altman plots ((d), (e) and (f))
-
Relaxation corrected simulated MM model for improved fitting and quantification of 1H FID MRSI data
Andrew Martin Wright1,2, Saipavitra Murali Manohar1,3, Theresia Ziegs1,2, and Anke Henning1,4
1Max Planck Institute for Biological Cybernetics, Tübingen, Germany, 2IMPRS for Cognitive and Systems Neuroscience, Tübingen, Germany, 3University of Tübingen, Faculty of Science, Tübingen, Germany, 4Advanced Imaging Research Center, UT Southwestern Medical Center, Dallas, TX, United States
A novel method to simulate macromolecule signals to improve MRSI metabolite mapping and quantification with very short TR 1H-FID MRSI. The method
developed is compared more commonly used methods of accounting for macromolecule
signals. Results show improved metabolite mapping.

Figure 4: Metabolite maps for the four approaches used for fitting MRSI data. Maps are reported with T1-relaxation corrections and in units of mmol / kg. It is apparent that using simulated MM basis vectors performs best generally when considering the poor fits of NAAG, mI, and Gln from Approach A and Approach B.

Figure 1: The
relaxation-corrected, sequence-specific MM simulation model algorithm diagram. Voigt lines are simulated using measured Gaussian and Lorentzian lineshapes. Voigt lines are then scaled by measured concentrations of MM from 9.4T and further processed with single-spin Bloch simulations to simulate a universal base MM spectrum which is then attenuated by sequence specific relaxation effects to yield a sequence specific MM basis vector.
-
Automatic phase order correction in challenging MR spectra
Maria Yanez Lopez1,2
1Centre for the Developing Brain, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 2Biomedical Engineering Department, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom
The aim of this work is
to develop an automatic zero and first order phase order correction and
apply it to challenging spectra, using an MRS LASER sequence at 3T

Fig 2. Top: Representative spectrum
following raw data reconstruction and spectral registration. Bottom: Fit
results using default preprocessing (left, TARQUIN) and proposed preprocessing pipeline (right,
Matlab). Inline
images display the effects of the phase correction step on the baseline.

Fig 1. Preprocessing pipeline (Matlab), including spectra alignment,
eddy current correction and the proposed automatic zero and first order phase correction.
-
Phase Correction in IDEAL-type Rapid Spectroscopic Imaging
Nour EL SABBAGH1, Carine CHASSAIN1, Hélène RATINEY2, Guilhem PAGES1, and Jean-Marie BONNY1
1INRAE, AgroResonance, UR QuaPA, F-63122, Saint-Gènes-Champanelle, France, 2University of Lyon, INSA‐Lyon, Université Claude Bernard Lyon 1, UJM Saint-Etienne, CNRS, Inserm, CREATIS UMR 5220, U1206, F‐69621, Lyon, France
In IDEAL-type sequences, sequence-dependent phase errors are likely to be accumulated alongside the CS's targeted phase, disturbing the spectral study. These phase errors are due to different frequency switching cases during the pulse sequence and slice or readout position shifting.

Figure 1: Illustration of the IDEAL SPIRAL spectral encoding scheme. It consists of Radiofrequency (RF) pulses applied during an excitation time (t1), and acquisition with spiral-OUT spatial encoding (t3-t2) applied after an echo time (TE=t2-t1). Several shots are used to encode the spectral information, which is targeted during the evolution time (TE), while slightly increasing the TE after each shot (TEm is the echo time of the mth shot). Three shots are presented, but this pulse sequence is true for m shots.

Figure
2: Illustration of the different cases of the emission/reception frequency switching during the pulse
sequence timing, leading to different frequency dependence
during the evolution times. Acq-Switch case: fe-fr switch before the acquisition at t2, and the CS
behaviour detection is done in reference to fe. RF-Switch case: fe-fr switch before the evolution time at t1, hence CS
behaviour detection done in reference to fr. Double 0-Switch case: fe-0 switch for the evolution time at t1, 0-fr switch at the end of it at t2.
-
Computation of Cramér-Rao Lower Bounds (CRLB) for spectral baseline shapes
Kelley M. Swanberg1, Martin Gajdošík1, Karl Landheer1, and Christoph Juchem1,2
1Biomedical Engineering, Columbia University School of Engineering and Applied Science, New York, NY, United States, 2Radiology, Columbia University Medical Center, New York, NY, United States
Here we treat spectral baselines as piecewise polynomial shapes akin to metabolite basis
functions to show that amplitude Cramér-Rao Lower Bounds (CRLB) can under some
circumstances offer precision estimates on baseline parameters themselves as well as increase metabolite CRLB accuracy.

Fig. 1. Partial derivatives of linear combination model with respect to complex baseline shapes for Fisher information matrix calculation. Shown here are the Fourier transforms of example real and imaginary polynomial and spline baseline components incorporated into the Fisher information matrix used to estimate Cramér-Rao Lower Bounds (CRLB) for linear combination model fits to simulated in vivo sLASER (TE 20.1 ms) metabolite proton spectra. Each shape is scaled by its corresponding polynomial coefficient for direct calculation of relative CRLBs. ppm: parts per million.

Fig. 5. Baseline Cramér-Rao Lower Bounds (CRLB) improved metabolite CRLB accuracy. Calculating amplitude CRLBs for polynomial or spline baselines directly from the Fisher information matrix improved
correspondence between metabolite amplitude CRLBs and parameter estimate standard deviations (S.D.) by SNR (before=blue; after=black). Correspondent
with Fig. 4, non-normal distributions (pink), for which S.D. may not be an appropriate measure of parameter variability, were observed more often for fits using spline than polynomial
baselines. ppm: parts per million.
-
Accounting for bias in estimated metabolite concentrations from cohort studies as caused by limiting the fitting parameter space
Rudy Rizzo1 and Roland Kreis1
1Department of Radiology and Biomedical Research, University of Bern, Bern, Switzerland
Limiting
the parameter space to meaningful values when fitting MR spectra introduces
bias in cohort averaging. A correction term can reduce this bias whereas extending
the parameter space can eliminate it.

Figure 2: Top: cohort distribution with unbounded
fitting algorithm and pertinent formulae. µ: ground truth mean, σ: ground
truth std. µTR: mean
of right truncated distribution, µTL:
mean of left truncated distribution.
Bottom: cohort distribution with 0+ fitting
boundary. Limiting parameter space skews the Gaussian distribution. The
negative tail is mapped to a small interval around 0+. Assuming its contribution
to equal 0, the true mean can be reconstructed from its distorted version.

Figure 3: histogram of estimated concentrations for
GABA in three different parameter space settings. Cohort 1 is depicted in the
left column and cohort 2 in the right. µGT: ground truth concentration. µdistr: distribution estimated concentration.
-
Data-driven bases optimization for fitting of in vivo MR spectra
Alexander Saunders1,2 and Stefan Bluml1,2
1Radiology, Children's Hospital Los Angeles/USC, Los Angeles, CA, United States, 2Rudi Schulte Research Institute, Santa Barbara, CA, United States
Simultaneous fitting of sets of in vivo spectra could potentially be used to optimize basis spectra

Table 1: Comparison of published [3] vs. optimized chemical shift positions and J-couplings for myo-inositol

Figure 1: Examples of individual 3T, PRESS TR=2000ms, TE=35ms spectra of abnormal tissue with prominent mI (A) and of normal grey matter (B). C: Myo-inositol basis spectra before and after optimization.
-
The effect of basis sets on the analysis of in vivo brain MRS data obtained with standard PRESS sequences
Martin Gajdošík1, Karl Landheer1, Kelley M. Swanberg1, Lawrence S. Kegeles2,3,4, Dikoma C. Shungu5, Camilo de la Fuente-Sandoval6,7, and Christoph Juchem1,4
1Department of Biomedical Engineering, Columbia University, New York City, NY, United States, 2Department of Psychiatry, Columbia University College of Physicians and Surgeons, New York City, NY, United States, 3New York State Psychiatric Institute, New York City, NY, United States, 4Department of Radiology, Columbia University Medical Center, New York City, NY, United States, 5Weill Cornell Medicine, New York City, NY, United States, 6Laboratory of Experimental Psychiatry, Instituto Nacional de Neurología y Neurocirugía, Mexico City, Mexico, 7Department of Neuropsychiatry, Instituto Nacional de Neurología y Neurocirugía, Mexico City, Mexico
The impact of using realistic basis set, simulated with accurate RF pulses, timings, and other sequence details, versus a less
realistic basis set, at the same TE is investigated here for PRESS spectra at 3
T. It is shown that inaccurate basis information leads to spectral quantification errors.

Figure 2: Example spectrum measured
with GE’s standard product implementation of the PRESS sequence and fitted with
four different PRESS basis sets of matched TE 35 ms. The original data are in black, the fit is depicted in red. The upper part of the figures represents the
residual signal after fitting. A – Matched GE basis set; B – Basis set based on
GE timings, but using hard-pulses; C – Basis set for Philips’ PRESS; D – Basis
set for the Siemens’ PRESS. Individual fits were printed from LCModel.

Figure 3: Example spectrum measured
with Siemens’s standard product implementation of the PRESS sequence and fitted
with four different PRESS basis sets of matched TE 35 ms. The original data are in black, the fit is depicted in red. The upper part of the figures represents
the residual signal after fitting. A – Matched Siemens basis set; B – Basis set
based on Siemens timings, but using hard-pulses; C – Basis set for Philips’
PRESS; D – Basis set for the GE’s PRESS. Individual fits were printed from LCModel.
-
Bayesian deep learning-based 1H-MRS of the brain: Metabolite quantification with uncertainty estimation using Monte Carlo dropout
HyeongHun Lee1 and Hyeonjin Kim1,2
1Department of Biomedical Sciences, Seoul National University, Seoul, Korea, Republic of, 2Department of Radiology, Seoul National University Hospital, Seoul, Korea, Republic of
The
proposed Bayesian deep learning-based approach in 1H-MRS of the
brain provides both metabolite content and corresponding uncertainty, and
therefore can be advantageous over the standard convolutional neural networks approaches in
consideration of clinical application.

Figure 1. The training of the BCNN and the estimation of metabolite
content and corresponding uncertainty. The metabolite content is estimated by multiple
regression using the metabolite basis set and the predictive mean spectrum that
is the mean spectrum over the BCNN-predicted metabolite-only spectra (number of
spectra = T (number of inferences)). The uncertainty in metabolite content is
estimated by multiple regression using the 2SD spectrum. In this case, the
metabolite basis set is used in absolute mode in accordance with the
2SD-spectrum.

Figure 2. (A) 4 representative simulated
spectra (BCNN input). (B) Ground
truth (GT) spectra. (C) BCNN-predicted
spectra. (D) Reconstructed spectra using the estimated metabolite content and metabolite
bases. (E) Difference spectra (GT – Predicted). (F) Difference spectra (Predicted – reconstructed). (G) Total uncertainty
spectra (= (H) aleatoric + (I) epistemic uncertainty) (BCNN-predicted
spectra shown in dotted line). (J)
2SD spectra. (K) Reconstructed 2SD
spectra using the estimated uncertainty and metabolite bases. (L) Difference spectra (2SD – reconstructed 2SD).
-
Impact of training size on deep learning performance in in vivo 1H MRS
Sungtak Hong1 and Jun Shen1
1National Institute of Mental Health, National Institutes of Health, Bethesda, MD, United States
The present study demonstrated that the benefit
of larger training data sizes could be marginal after reaching a threshold
number of datasets in training a convolutional neural network to restore degraded in vivo 1H MRS spectra.

Figure 1. Schematic overview
illustrating the generation of dataset and the proposed network architecture featuring
consecutive three convolutional blocks. A pair of 1D convolutional layer and batch
normalization layer act as a fundamental component with four times repetitions
for completing each block. Network training was conducted with pairs of ground
truth spectra and progressively degraded spectra while minimizing the mean
squared error using Adam optimization algorithm. Learning rate was set to 10-4.

Figure 2. Numerically calculated 1H
MRS spectra at low SNR (left column) and high SNR (right column). CNN-predicted
spectra, difference spectra (ground truth – predicted), and NMSE illustrate the
impact from using different training sizes in CNN.
-
Application of Deep Leaning Model for Quality Control of Short-echo 7T MRSI with Various Disease Types
Huawei Liu1, Emily Xie1, Helene Ratiney2, Michael Sdika2, and Yan Li1
1Department of Radiology and Biomedical Imaging, University of California, San Francisco, San Francisco, CA, United States, 2Univ. Lyon, INSA-Lyon, Université Claude Bernard Lyon 1, UJM-Saint Etienne, CNRS, Inserm, Lyon, France
Deep learning approach for artifacts filtering was explored and applied on in vivo 7T MRSI datasets acquired from healthy controls and patients with various diseases. An AUC of 0.966 was consistently achieved with different inputs combinations. Ongoing work is in progress for better metrics.

Figure 1. The convolutional neuronal network diagram for taking 3 tiles separated real and magnitude spectra as inputs. The final output value indicates the probability for bad label.

Figure 2. Models with different spectra inputs and tiles and the tested ACC and AUC results. No difference was found between including or not tissue ratios.
-
Deep Learning Using Synthetic Data for Signal Denoising and Spectral Fitting in Deuterium Metabolic Imaging
Abidemi Adebayo1, Keshav Datta2, Ronald Watkins2, Shie-Chau Liu2, Ralph Hurd2, and Daniel Mark Spielman2
1Mechanical Engineering, Stanford University, Stanford, CA, United States, 2Radiology, Stanford University, Stanford, CA, United States
Deuterium metabolic imaging, a promising tool to probe in vivo glucose metabolism, is severely limited by SNR. In this work we show that an autoencoder network trained using only synthetic data can reduce noise and provide a good spectral fit.

Figure 3 Reconstructed spectra from the neural network (dotted blue lines),
compared with the spectra from human brain obtained 15, 45, 75 and 105 minutes
post oral ingestion of deuterated glucose (solid red lines).

Figure 1 Autoencoder architecture used for denoising and fitting the spectrum.
-
Deep Learning Based MRS Metabolite Quantification: CNN and ResNet versus Non Linear Least Square Fitting
Federico Turco1, Irena Zubak2, and Johannes Slotboom1
1Institute of Diagnostic and Interventional Neuroradiology / SCAN, University Hospital Bern and Inselspital, University Bern, Bern, Switzerland, 2Neurosurgery, University Hospital Bern and Inselspital, University Bern, Bern, Switzerland
Deep learning based metabolite quantification of in vivo MRSI data using CNN and ResNet were performed and compared to traditional NLLS-quantification. Accuracy measures were given, and both methods seem a viable alternative state of the art NLLS quantification.

Figure 3: Metabolite concentration mapping for Ace, Choline, and Creatine in rows 1, 2, and 3 respectively. Obtained by the three different methods, in (a) healthy brain spectra while (b) is a brain tumor.

Figure 1: Representation of both implemented neural networks, an CNN (a) and a ResNet (b). In both cases, the input and output are exactly the same, and all the convolutional layers have the same kernel size of 3.
-
Quantification of 2D-MRSI Datasets using Random Forest Regression Comparing to Prior Knowledge Based Spectral Fitting applied to Brain Tumors
Brigitte Schweisthal1, Federico Turco1, Raphael Meier1, Irena Zubak2, and Johannes Slotboom1
1Neuroradiology / Support Center for Advanced Neuroimaging (SCAN), University Hospital and Inselspital, University Bern, Bern, Switzerland, 2Neurosurgery, University Hospital and Inselspital, University Bern, Bern, Switzerland
This work deals with quantification of clinical
1H-MRSI data using machine learning. RF-regressors
were determined based on 10000 simulated TD & FD responses obeying a prior
knowledge model. RF-regression is a valid alternative for quantification with comparative accuracy as NLLS-fitting.

Figure 3: The first column displays the GT peak area maps as found by TDFDFit. The second column displays the RF-regressor predicted maps for the noise level 0.5 of the in vivo semiLASER data sets. The third and the fourth column show the predicted maps of noise level = 4 and noise level = 0.5. Example signals with very poor and extreme poor SNR are displayed in Figure 4.

Figure 4: This figure shows the x-y-scatter plots for NAA, Cho, Cr, and Glu peak area parameters: horizontally the GT value obtained with TDFDFit, and vertically the RF-regressor predicted area parameter values. For NAA the coefficient of determination is best namely R2=0.991, for Cho -> R2=0.988 ,for Cr -> R2=0.989 and for Glu the worst namely R2=0.975. Note that the slope of all linear regression lines is between 0.96 for NAA and maximum 1.26 for Glu, in accordance with Cramér-Rao minimum variance bounds.
-
In vivo Cerebellum MRSI reconstruction by domain-transform manifold learning
Neha Koonjoo1,2,3, Adam Berrington4, Bo Zhu2,3,5, Uzay E Emir6,7, and Matthew S Rosen2,3,5
1Department of Radiology, A.A Martinos Center for Biomedical Imaging / MGH, Charlestown, MA, United States, 2Harvard Medical School, Boston, MA, United States, 3Department of Physics, Harvard University, Cambridge, MA, United States, 4Sir Peter Mansfield Imaging Centre, School of Physics and Astronomy, University of Nottingham, Nottingham, United Kingdom, 5Radiology, A.A Martinos Center for Biomedical Imaging / MGH, Charlestown, MA, United States, 6School of Health Sciences, Purdue University, West Lafayette, IN, United States, 7Weldon School of Biomedical Engineering, Purdue University, West Lafayette, IN, United States
A deep neural network based on the AUTOMAP formalism to reconstruct metabolic cycle FIDs into spectral domain. Density matrix formalism was used to generate up/downfields of 1H FIDs of 27 metabolites. The proposed strategy was validated on noisy simulated FIDs and an in vivo cerebellum 3T data.

Figure 1a: Proposed strategy to learn the entire end-to-end inverse function and low dimensional representations of spectroscopic signals – (from left to right) Building the training database: The 27 metabolites FIDs were simulated with a sLASER pulse sequence with metabolic cycling and B0 variations. The simulated metabolites FIDs were used to create the training database by combining metabolites, water signal, phase modulations and 20-50dB of gaussian noise. The input/output to the network was the real and imaginary component of metabolic cycle FIDs/spectra (see Methods).

Figure 3: In vivo cerebellum MRSI reconstruction with AUTOMAP. (from top to bottom) The AUTOMAP and NUFFT reconstructed summed image from the 1st time point are shown. The metabolite-only spectra with a range from 0.5 to 4.2 ppm from the 9 different voxels (represented by the black box in the images) are displayed in blue for AUTOMAP and in black for NUFFT. At the bottom an enlarged spectra with the corresponding metabolite peaks (total Choline (tCho), NAA (tNAA) and Creatine (tCr) is represented.
-
On the quantification of the striatum neurochemical profile using STEAM MRS: a comparison of 3T versus 7T in a cohort of elderly subjects
Ana Gogishvili1,2, Christopher E. J. Doppler3,4, Ezequiel Farrher1, Aline Seger3,4, Michael Sommerauer3,4, Ketevan Kotetishvili2, and N. Jon Shah1,5,6,7
1Institute of Neuroscience and Medicine 4, Medical Imaging Physics, Forschungszentrum Jülich, Jülich, Germany, 2Engineering Physics Department, Georgian Technical University, Tbilisi, Georgia, 3Institute of Neuroscience and Medicine 3, Forschungszentrum Jülich, Jülich, Germany, 4University of Cologne, Faculty of Medicine and University Hospital Cologne, Department of Neurology, Cologne, Germany, 5Institute of Neuroscience and Medicine 11, Forschungszentrum Jülich, Jülich, Germany, 6JARA BRAIN Translational Medicine, RWTH Aachen University, Aachen, Germany, 7Department of Neurology, Faculty of Medicine, RWTH Aachen University, Aachen, Germany
We quantified the neurochemical profile of the human striatum in vivo in healthy control subjects acquired with a single voxel STEAM MRS sequence at 3T and 7T. To this end, we quantified the tissue differences for 12 reliably detected metabolites.

Figure 4. The mean metabolite concentrations across the whole group of subjects, for methods M1 (a), M3 (b), and the CRLB values (c). Total concentrations tCho=GPC+PCh, tNAA=NAA+NAAG, tCr=Cr+PCr and Glx=Glu+Gln are additionally shown.

Figure 3. Linear regression (green line) estimated for tCr (a), Glu (b), GSH (c), Ins (d), NAA (e), tCho (f) using pooled 3T and 7T data. Metabolite concentrations of individual subjects determined from pooled results (3T and 7T) and the calculated α value for each metabolite. Different shapes represent different brain areas (o: striatum; ⧠: frontal WM; ◊: parietal WM; *: occipital WM). Blue and red points represent data from 7T and 3T, respectively. The green shaded area highlights the 95% confidence band.
-
The influence of spectral registration on diffusion-weighted magnetic resonance spectroscopy ADC estimates.
Christopher W Jenkins1
1CUBRIC, Cardiff University, Cardiff, United Kingdom
Simulated data are used to examine spectral registration and its new robust iteration in the context of diffusion-weighted MRS. The accuracy of these methods is examined across a broad range of SNR, and the effect they have on ADC estimates, investigated.

Fig.1: Frequency correction fidelity for SR and RSR with two increments of direct averaging. A frequency correction fidelity of 1 indicates perfect correction, 0 indicates correction was as effective as no correction, and a value less than 0 is worse than no correction. RSR performs better for low b data than high b-value data, indicating a potential for bias in diffusion fits. While DA provides a marginal gain in the effective domain of both SR and RSR, it compromises the fidelity of higher SNR data.

Fig.4: Histograms of the percentage deviation from known the ADC. Data are pooled from the fits of TNAA, TCho, and MyI, and diffusion fits with $$$R^2$$$<0.75 were excluded. The blue bars represent fits of all data, while orange bars are data fit after excluding points with SNR < 2. Here a negative value indicates an underestimation of the ADC, while a positive value indicates overestimation. All methods tended to overestimation, suggesting that higher b-values were disproportionately affected by incoherent averaging. However, filtering based on SNR remedies this to an extent.